2.3. Основные показатели ремонтопригодности

При количественном описании этого свойства, которое присуще только восстанавливаемому объекту, время восстановления является случайной величиной, зависящей от целого ряда факторов: характера возникшего отказа; приспособленности объекта (устройства, установки и др.) к быстрому обнаружению отказа; квалификации обслуживающего персонала; наличия технических средств; быстроты замены отказавшего элемента в объекте и др. Время восстановления - это время, затраченное на обнаружение, поиск причины отказа и устранения последствий отказа. Опыт показывает, что в сложных электроустановках (системах) 70-90% времени восстановления приходится на поиск отказавшего элемента [2, 15, 16, 17].

2.3.1. Среднее время восстановления

Среднее время восстановления - это математическое ожидание времени восстановления работоспособного состояния объекта после отказа . Из определения следует, что

где n - число восстановлений, равное числу отказов; - время, затраченное на восстановление (обнаружение, поиск причины и устранение отказа), в часах.

Показатель можно определить и на основании статистических данных, полученных для М однотипных восстанавливаемых объектов. Структура расчетной формулы остается той же:

где М - количество однотипных объектов, для каждого из которых определено общее время восстановления за заданное время наблюдений;
, где - время восстановления j-го объекта после i-го отказа; nj - количество восстановлений j-го объекта за время наблюдений, причем .

2.3.2. Интенсивность восстановления

Интенсивность восстановления - это отношение условной плотности вероятности восстановления работоспособного состояния объекта, определенной для рассматриваемого момента времени при условии, что до этого момента восстановление не было завершено, к продолжительности этого интервала.

Статистическая оценка этого показателя находится как

где n_в(Dt) - количество восстановлений однотипных объектов за интервал Dt; - среднее количество объектов, находящихся в невосстановленном состоянии на интервале Dt.

В частном случае, когда интенсивность восстановления постоянна, то есть m(t) =m= const, вероятность восстановления за заданное время t подчиняется экспоненциальному закону [3, 13, 21] и определяется по выражению

Этот частный случай имеет наибольшее практическое значение, поскольку реальный закон распределения времени восстановления большинства электроэнергетических объектов (поток восстановлений) близок к экспоненциальному [10, 14]. Используя свойства этого распределения, запишем очень важную зависимость:

В дальнейшем эта взаимосвязь между Т_в и m будет часто использоваться при анализе восстанавливаемых систем.

При более детальных расчетах показателей надежности ремонтируемых (восстанавливаемых) объектов определяется такой показатель ремонтопригодности, как процентное время восстановления g. Это время в течение которого восстановление работоспособности объекта будет осуществлено с вероятностью g , выраженной в процентах [7].

2.4. Комплексные показатели надежности

2.4.1. Коэффициент готовности

Процесс функционирования восстанавливаемого объекта можно представить как последовательность чередующихся интервалов работоспособности и восстановления (простоя).

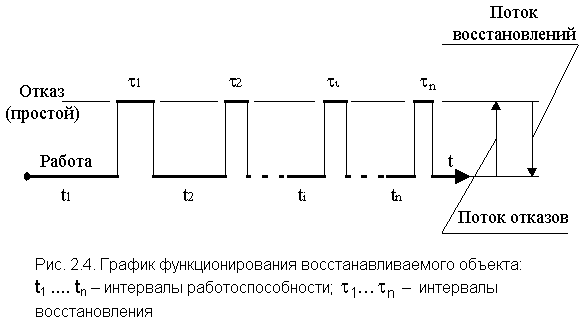
Коэффициент готовности - это вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается [7]. Математическое определение этого показателя дано ниже (разд. 7) при анализе надежности восстанавливаемых систем.

Этот показатель одновременно оценивает свойства работоспособности и ремонтопригодности объекта.

Для одного ремонтируемого объекта коэффициент готовности

Из выражения 2.23 видно, что коэффициент готовности объекта может быть повышен за счет увеличения наработки на отказ и уменьшения среднего времени восстановления. Для определения коэффициента готовности необходим достаточно длительный календарный срок функционирования объекта.

Зависимость коэффициента готовности от времени восстановления затрудняет оценку надежности объекта, так как по К_Г нельзя судить о времени непрерывной работы до отказа. К примеру, для одного и того же численного значения К_Г можно иметь малые интервалы и t_i (см. рис. 2.4) и значительно большие. Таким образом можно доказать, что на конкретном интервале работоспособности вероятность безотказной работы будет больше там, где больше t_i, хотя за этим интервалом может последовать длительный интервал простоя . Коэффициент готовности является удобной характеристикой для объектов, которые предназначены для длительного функционирования, а решают поставленную задачу в течение короткого промежутка времени (находятся в ждущем режиме), например, релейная защита, контактная сеть (особенно при относительно малых размерах движения), сложная контрольная аппаратура и т.д.

2.4.2. Коэффициент оперативной готовности

Коэффициент оперативной готовности К_ОГопределяется как вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени (кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается) и, начиная с этого момента, будет работать безотказно в течение заданного интервала времени.

Из вероятностного определения следует, что

где К_Г - коэффициент готовности; Р(t_р) - вероятность безотказной работы объекта в течение времени (t_р), необходимого для безотказного использования по назначению.

Для часто используемого в расчетной практике простейшего потока отказов, когда

l = w ,Р(t_р) соответственно определяется по выражению

2.4.3. Коэффициент технического использования

Коэффициент технического использования К_ТИравен отношению математического ожидания суммарного времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к математическому ожиданию суммарного времени пребывания объекта в работоспособном состоянии и простоев, обусловленных техническим обслуживанием и ремонтом за тот же период эксплуатации:

где t_i - время сохранения работоспособности в i-м цикле функционирования объекта; - время восстановления (ремонта) после i-го отказа объекта; - длительность выполнения j-й профилактики, требующей вывода объекта из работающего состояния (использования по назначению); n - число рабочих циклов за рассматриваемый период эксплуатации; m - число отказов (восстановлений) за рассматриваемый период; k - число профилактик, требующих отключения объекта в рассматриваемый период.

Как видно из выражения (2.25), коэффициент технического использования характеризует долю времени нахождения объекта в работоспособном состоянии относительно общей (календарной) продолжительности эксплуатации. Следовательно, К_ТИотличается от К_Гтем, что при его определении учитывается все время вынужденных простоев, тогда как при определении К_Гвремя простоя, связанное с проведением профилактических работ, не учитывается.

Суммарное время вынужденного простоя объекта обычно включает время:

- на поиск и устранение отказа;

- на регулировку и настройку объекта после устранения отказа;

- для простоя из-за отсутствия запасных элементов;

- для профилактических работ.

В условиях эксплуатации на уровень надежности объектов большое влияние оказывают техническое обслуживание и ремонт. Подробно техническое обслуживание и ремонт, стратегии их организации и их решающее влияние на надежность рассматриваются в [1, 16].

ГОСТ 27.002-89 содержит кроме проанализированных в
данном пособии наиболее употребляемых показателей надежности и другие показатели: среднюю трудоемкость восстановления, средний срок сохраняемости, гамма-процентный ресурс, гамма-процентное время восстановления, гамма-процентный срок сохраняемости и др. При необходимости определения указанных показателей используются специальные методики, где процедура расчета основывается на тех же законах математической статистики и теории вероятностей, по которым определяются и более широко используемые показатели надежности.

3.1. Распределение Вейбулла

Опыт эксплуатации очень многих электронных приборов и значительного количества электромеханической аппаратуры показывает, что для них характерны три вида зависимостей интенсивности отказов от времени (рис. 3.1), соответствующих трем периодам жизни этих устройств [3, 8, 10, 19].

Нетрудно увидеть, что этот рисунок аналогичен рис. 2.3, так как график функции l (t) соответствует закону Вейбулла. Указанные три вида зависимостей интенсивности отказов от времени можно получить, используя для вероятностного описания случайной наработки до отказа двухпараметрическое распределение Вейбулла [12, 13, 15]. Согласно этому распределению плотность вероятности момента отказа

где d - параметр формы (определяется подбором в результате обработки экспериментальных данных, d > 0); l - параметр масштаба,

.

Интенсивность отказов определяется по выражению

Вероятность безотказной работы

а средняя наработки до отказа

Отметим, что при параметре d= 1 распределение Вейбулла переходит в экспоненциальное, а при d= 2 - в распределение Рэлея.

При d<1 интенсивность отказов монотонно убывает (период приработки), а при монотонно возрастает (период износа), см. рис. 3.1. Следовательно, путем подбора параметра d можно получить, на каждом из трех участков, такую теоретическую кривую l (t), которая достаточно близко совпадает с экспериментальной кривой, и тогда расчет требуемых показателей надежности можно производить на основе известной закономерности.

Распределение Вейбулла достаточно близко подходит для ряда механических объектов (к примеру, шарикоподшипников), оно может быть использовано при ускоренных испытаниях объектов в форсированном режиме [12].

3.2. Экспоненциальное распределение

Как было отмечено в подразд. 3.1 экспоненциальное распределение вероятности безотказной работы является частным случаем распределения Вейбулла, когда параметр формы d = 1. Это распределение однопараметрическое, то есть для записи расчетного выражения достаточно одного параметра l = const . Для этого закона верно и обратное утверждение: если интенсивность отказов постоянна, то вероятность безотказной работы как функция времени подчиняется экспоненциальному закону:

Среднее время безотказной работы при экспоненциальном законе распределения интервала безотказной работы выражается формулой:

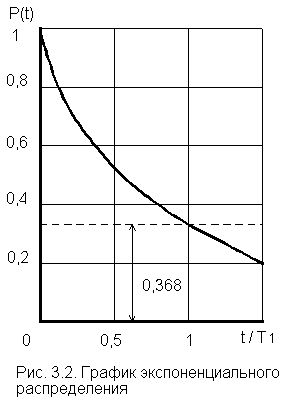
Заменив в выражении (3.5) величину l величиной 1 / Т₁, получим . (3.7)

Отметим, что вероятность безотказной работы на интервале, превышающем среднее время Т₁, при экспоненциальном распределении будет менее 0,368:

Р(Т₁) == 0,368 (рис. 3.2).

Длительность периода нормальной эксплуатации до наступления старения может оказаться существенно меньше Т₁, то есть интервал времени на котором допустимо пользование экспоненциальной моделью, часто бывает меньшим среднего времени безотказной работы, вычисленного для этой модели. Это легко обосновать, воспользовавшись дисперсией времени безотказной работы. Как известно [4, 13], если для случайной величины t задана плотность вероятности f(t) и определено среднее значение (математическое ожидание) Т₁, то дисперсия времени безотказной работы находится по выражению:

и для экспоненциального распределения соответственно равна:

После некоторых преобразований получим:

Таким образом, наиболее вероятные значения наработки, группирующиеся в окрестности Т₁, лежат в диапазоне, то есть в диапазоне от t = 0 до t = 2Т₁. Как видим, объект может отработать и малый отрезок времени и время

t = 2Т₁, сохранив l = const. Но вероятность безотказной работы на интервале 2Т₁ крайне низка:

.

Важно отметить, что если объект отработал предположим, время t без отказа, сохранив l = соnst, то дальнейшее распределение времени безотказной работы будет таким, как в момент первого включения l = соnst.

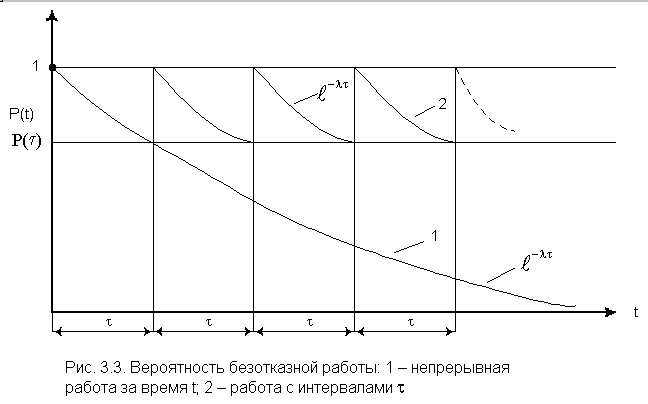
Таким образом, отключение работоспособного объекта в конце интервала и новое его включение на такой же интервал множество раз приведет к пилообразной кривой (см. рис. 3.3).

Другие распределения не имеют указанного свойства. Из рассмотренного следует на первый взгляд парадоксальный вывод: поскольку за все время t устройство не стареет (не меняет своих свойств), то нецелесообразно проводить профилактику или замену устройств для предупреждения внезапных отказов, подчиняющихся экспоненциальному закону. Конечно, никакой парадоксальности этот вывод не содержит, так как предположение об экспоненциальном распределении интервала безотказной работы означает, что устройство не стареет. С другой стороны, очевидно, что чем больше время, на которое включается устройство, тем больше всевозможных случайных причин, которые могут вызвать отказ устройства. Это весьма важно для эксплуатации устройств, когда приходится выбирать интервалы, через которые следует производить профилактические работы с тем, чтобы сохранить высокую надежность работы устройства. Этот вопрос подробно рассматривается в работе [1].

Модель экспоненциального распределения часто используется для априорного анализа, так как позволяет не очень сложными расчетами получить простые соотношения для различных вариантов создаваемой системы. На стадии апостериорного анализа (опытных данных) должна проводиться проверка соответствия экспоненциальной модели результатам испытаний. В частности, если при обработке результатов испытаний окажется, что , то это является доказательством экспоненциальности анализируемой зависимости.

На практике часто бывает, что l№const,однако, и в этом случае его можно применять для ограниченных отрезков времени. Это допущение оправдывается тем, что при ограниченном периоде времени переменную интенсивность отказов без большой ошибки можно заменить [12, 15] средним значением:

3.3. Распределение Рэлея

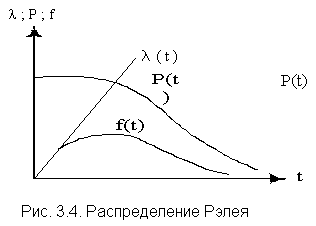
Плотность вероятности в законе Рэлея (см. рис. 3.4) имеет следующий вид

где d* - параметр распределения Рэлея (равен моде этого распределения [13]). Его не нужно смешивать со среднеквадратическим отклонением:

.

Интенсивность отказов равна:

Характерным признаком распределения Рэлея является прямая линия графика l(t), начинающаяся с начала координат.

Вероятность безотказной работы объекта в этом случае определится по выражению

Средняя наработка до отказа

3.4. Нормальное распределение (распределение Гаусса)

Нормальный закон распределения характеризуется плотностью вероятности вида

где m_x, s_x - соответственно математическое ожидание и среднеквадратическое отклонение случайной величины х.

При анализе надежности электроустановок в виде случайной величины, кроме времени, часто выступают значения тока, электрического напряжения и других аргументов. Нормальный закон - это двухпараметрический закон, для записи которого нужно знать m_x и s_x.

Вероятность безотказной работы определяется по формуле

а интенсивность отказов - по формуле

На рис. 3.5 изображены кривые l(t), Р(t) и¦ (t) для случая s_t<< m_t, характерного для элементов, используемых в системах автоматического управления [3].

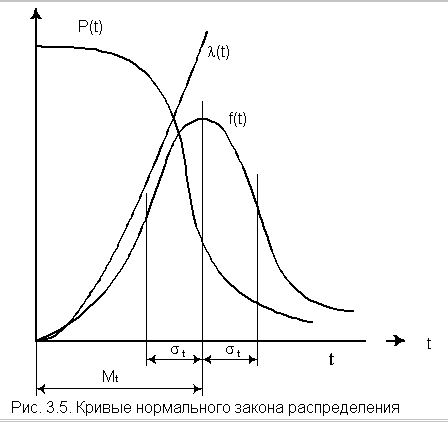
В данном пособии показаны только наиболее распространенные законы распределения случайной величины. Известен целый ряд законов, так же используемых в расчетах надежности [4, 9, 11, 13, 15, 21]: гамма-распределение, -распределение, распределение Максвелла, Эрланга и др.

Следует отметить, что если неравенство s_t<< m_t не соблюдается, то следует использовать усеченное нормальное распределение [19].

Для обоснованного выбора типа практического распределения наработки до отказа необходимо большое количество отказов с объяснением физических процессов, происходящих в объектах перед отказом.

В высоконадежных элементах электроустановок, во время эксплуатации или испытаний на надежность, отказывает лишь незначительная часть первоначально имеющихся объектов. Поэтому значение числовых характеристик, найденное в результате обработки опытных данных, сильно зависит от типа предполагаемого распределения наработки до отказа. Как показано в [13,15], при различных законах наработки до отказа, значения средней наработки до отказа, вычисленные по одним и тем же исходным данным, могут отличаться в сотни раз. Поэтому вопросу выбора теоретической модели распределения наработки до отказа необходимо уделять особое внимание с соответствующим доказательством приближения теоретического и экспериментального распределений (см. разд. 8).

Определим показатели надежности для наиболее часто используемых законов распределения времени возникновения отказов.

3.5.1. Определение показателей надежности при экспоненциальном законе распределения

Пример. Пусть объект имеет экспоненциальное распределение времени возникновения отказов с интенсивностью отказов l = 2,5 Ч 10^-5 1/ч.

Требуется вычислить основные показатели надежности невосстанавливаемого объекта за t = 2000 ч.

Решение.

1. Вероятность безотказной работы за время t = 2000 ч равна




2. Вероятность отказа за t = 2000 ч равна

3. Используя выражение (2.5), вероятность безотказной работы в интервале времени от 500 ч до 2500 ч при условии, что объект проработал безотказно 500 ч равна

.

4. Средняя наработка до отказа

ч.

3.5.2. Определение показателей надежности при распределении Рэлея

Пример. Параметр распределения d* = 100 ч.

Требуется определить для t = 50 ч величины P(t), Q(t), l (t),Т₁.

Решение.

Воспользовавшись формулами (3.11), (3.12), (3.13), получим

3.5.3. Определение показателей схемы при распределении Гаусса

Пример. Электрическая схема собрана из трех последовательно включенных типовых резисторов: ;

(в % задано значение отклонения сопротивлений от номинального).

Требуется определить суммарное сопротивление схемы с учетом отклонений параметров резисторов.

Решение.

Известно, что при массовом производстве однотипных элементов плотность распределения их параметров подчиняется нормальному закону [15]. Используя правило 3s (трех сигм), определим по исходным данным диапазоны, в которых лежат значения сопротивлений резисторов: ; 

Следовательно,

Когда значения параметров элементов имеют нормальное распределение, и элементы при создании схемы выбираются случайным образом, результирующее значение Rеявляется функциональной переменной, распределенной так же по нормальному закону [12, 15], причем дисперсия результирующего значения, в нашем случае , определяется по выражению

Поскольку результирующее значение Rераспределено по нормальному закону, то, воспользовавшись правилом 3s , запишем

где - номинальные паспортные параметры резисторов.

Таким образом

Данный пример показывает, что при увеличении количества последовательно соединенных элементов результирующая погрешность уменьшается. В частности, если суммарная погрешность всех отдельных элементов равна ± 600 Ом, то суммарная результирующая погрешность равна ± 374 Ом. В более сложных схемах, например в колебательных контурах, состоящих из индуктивностей и емкостей, отклонение индуктивности или емкости от заданных параметров сопряжено с изменением резонансной частоты, и возможный диапазон ее изменения можно предусмотреть методом, аналогичным с расчетом резисторов [15].

3.5.4. Пример определения показателей надежности неремонтируемого объекта по опытным данным

Пример. На испытании находилось N_о = 1000 образцов однотипной невосстанавливаемой аппаратуры, отказы фиксировались через каждые 100 часов.

Требуется определить в интервале времени от 0 до 1500 часов. Число отказов на соответствующем интервале представлено в табл. 3.1.

Номер i-го  интервала	,ч	шт.		,1/ч
1	0 -100	50	0,950
2	100 -200	40	0,910	0,430
3	200 -300	32	0,878	0,358
4	300 - 400	25	0,853	0,284
5	400 - 500	20	0,833	0,238
6	500 - 600	17	0,816	0,206
7	600 -700	16	0,800	0,198
8	700 - 800	16	0,784	0,202
9	800 - 900	15	0,769	0,193
10	900 -1000	14	0,755	0,184
11	1000 -1100	15	0,740	0,200
12	1100 -1200	14	0,726	0,191
13	1200 -1300	14	0,712	0,195
14	1300 -1400	13	0,699	0,184
15	1400 -1500	14	0,685	0,202 Ч

Решение.

Согласно формуле (2.1) для любого отрезка времени, отсчитываемого от t = 0,

где t_i - время от начала испытаний до момента, когда зафиксировано n(t_i) отказов.

Подставляя исходные данные из табл. 3.1, получим:

Воспользовавшись формулой (2.9), получим значение , 1/ч:

Средняя наработка до отказа, при условии отказов всех N_o объектов, определяется по выражению

где tj - время отказа j-го объекта ( j принимает значения от 0 до N_о).

В данном эксперименте из N_о = 1000 объектам отказало всего объектов. Поэтому по полученным опытным данным можно найти только приближенное значение средней наработки до отказа. В соответствии с поставленной задачей воспользуемся формулой из [13]:

при r Ј N_о , (3.16)

где tj - наработка до отказа j-го объекта ( j принимает значения
от 1 до r); r - количество зафиксированных отказов (в нашем случае r = 315); tr - наработка до r-го (последнего) отказа.

Полагаем, что последний отказ зафиксирован в момент окончания эксперимента (tr = 1500).

На основе экспериментальных данных суммарная наработка объектов до отказа равна

где - среднее время наработки до отказа объектов, отказавших на интервале .

В результате

Примечание: обоснование расчетов , по ограниченному объему опытных данных, изложено в разд. 8.

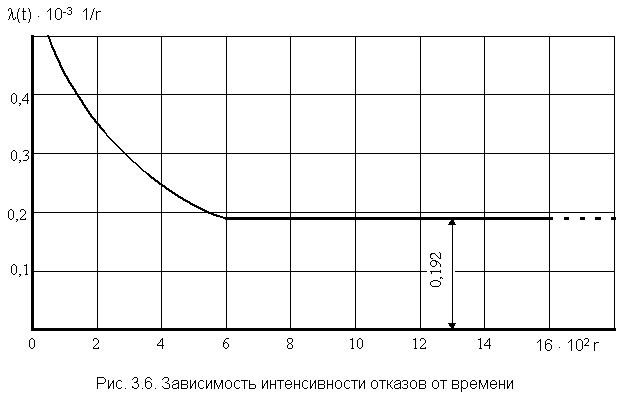
По полученным данным (см. табл. 3.1) построим график l(t).

Из графика видно, что после периода приработки t і 600 ч интенсивность отказов приобретает постоянную величину. Если предположить, что и в дальнейшем l будет постоянной, то период нормальной эксплуатации связан с экспоненциальной моделью наработки до отказа испытанного типа объектов. Тогда средняя наработка до отказа

Таким образом, из двух оценок средней наработки до отказа
= 3831 ч и T₁ = 5208 ч надо выбрать ту, которая более соответствует фактическому распределению отказов. В данном случае можно предполагать, что если бы провести испытания до отказа всех объектов, то есть r = N_о, достроить график рис. 3.6 и выявить время, когда l начнет увеличиваться, то для интервала нормальной эксплуатации (l = const) следует брать среднюю наработку до отказа T₁ = 5208 ч.

В заключение по данному примеру отметим, что определение средней наработки до отказа по формуле (2.7), когда r << N_о, дает грубую ошибку. В нашем примере

Если вместо N_о поставим количество отказавших объектов
r = 315, то получим

В последнем случае не отказавшие за время испытания объекты в количестве N_о - r = 1000-315 = 685 шт. вообще в оценку не попали, то есть была определена средняя наработка до отказа только 315 объектов. Эти ошибки достаточно распространены в практических расчетах.